 (A)
(A)
 (B)
(B)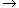 A
A B.
This proof will illustrate some of the more advanced features of Proof
Designer.
B.
This proof will illustrate some of the more advanced features of Proof
Designer.
The instructions below will lead you through a proof that
 (A)
(A)
 (B)
(B)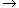 A
A B.
This proof will illustrate some of the more advanced features of Proof
Designer.
B.
This proof will illustrate some of the more advanced features of Proof
Designer.
 (A)
(A)
 (B)
(B)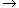 A
A B
and click the Set Conclusion button. (To type the power set symbol
B
and click the Set Conclusion button. (To type the power set symbol
 , type alt-shift-P (Windows) or
option-shift-P (Macintosh), or use
the symbol palette. To type the arrow
, type alt-shift-P (Windows) or
option-shift-P (Macintosh), or use
the symbol palette. To type the arrow 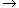 ,
type alt-C (Windows) or option-C (Macintosh), or use the symbol palette.)
There are no hypotheses for this theorem. Click OK.
,
type alt-C (Windows) or option-C (Macintosh), or use the symbol palette.)
There are no hypotheses for this theorem. Click OK.
 (A)
(A)
 (B)
(B) A
A B
and choose Direct from the Strategy menu. Proof Designer will suppose that
B
and choose Direct from the Strategy menu. Proof Designer will suppose that
 (A)
(A)
 (B) and it will
say that you must
now prove that A
(B) and it will
say that you must
now prove that A B.
B.
 (A)
(A)
 (B) and choose
Reexpress from the Strategy menu. Click on the Apply Definition button,
but don't click on OK yet. Proof Designer will rewrite the statement
as
(B) and choose
Reexpress from the Strategy menu. Click on the Apply Definition button,
but don't click on OK yet. Proof Designer will rewrite the statement
as  a(a
a(a
 (A)
(A) a
a
 (B)).
Now use the mouse to select the statement a
(B)).
Now use the mouse to select the statement a
 (A),
which appears before the
(A),
which appears before the  . (You do this
just the way you would do it in a word processing program, by dragging the
mouse across what you want
to select.) Click Apply Definition again and Proof Designer will change
a
. (You do this
just the way you would do it in a word processing program, by dragging the
mouse across what you want
to select.) Click Apply Definition again and Proof Designer will change
a
 (A) to a
(A) to a A, writing out the
definition of power set. Use the same procedure to write out
a
A, writing out the
definition of power set. Use the same procedure to write out
a
 (B) as a
(B) as a B, and then click
OK.
B, and then click
OK.
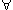 a(a
a(a A
A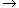 a
a B) and
choose Universal Instantiation from the Infer menu. When the dialog box
appears, say that you want to substitute A for a.
Proof Designer will infer
A
B) and
choose Universal Instantiation from the Infer menu. When the dialog box
appears, say that you want to substitute A for a.
Proof Designer will infer
A A
A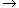 A
A B.
B.
 A
A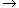 A
A B,
shift-click to select the goal A
B,
shift-click to select the goal A B as well, and choose
Modus Ponens from the Infer menu. Proof Designer will use the modus
ponens
inference rule to work backwards from the goal. Proof Designer will say
that you can infer the goal A
B as well, and choose
Modus Ponens from the Infer menu. Proof Designer will use the modus
ponens
inference rule to work backwards from the goal. Proof Designer will say
that you can infer the goal A B by modus ponens from
A
B by modus ponens from
A A
A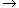 A
A B and
A
B and
A A, but you must still
prove A
A, but you must still
prove A A.
A.
 A
where Proof Designer says it is needed, it might be better to indicate
somehow that this is a general fact about all sets, and not a fact about
this specific set A. To do this, click on the sentence
“Suppose
A
where Proof Designer says it is needed, it might be better to indicate
somehow that this is a general fact about all sets, and not a fact about
this specific set A. To do this, click on the sentence
“Suppose
 (A)
(A)
 (B)” at the
beginning of the
proof. This selects the entire subproof that is introduced by this
sentence, along with the conclusion it justifies. (You can also do this
by clicking in the margin to the left of this subproof, or on the
conclusion it justifies.) Choose Insert from the Edit menu. This will
allow you to insert some new steps before the subproof you have just
selected. A dialog box will appear, asking what goal you want to achieve
with these additional steps. Click on the choice saying that you want to
prove something, and type in
(B)” at the
beginning of the
proof. This selects the entire subproof that is introduced by this
sentence, along with the conclusion it justifies. (You can also do this
by clicking in the margin to the left of this subproof, or on the
conclusion it justifies.) Choose Insert from the Edit menu. This will
allow you to insert some new steps before the subproof you have just
selected. A dialog box will appear, asking what goal you want to achieve
with these additional steps. Click on the choice saying that you want to
prove something, and type in 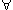 x(x
x(x x) as
the statement you want to prove. (To type
x) as
the statement you want to prove. (To type 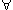 , you can type
alt-shift-A (Windows) or option-shift-A (Macintosh) or use the symbol
palette.) Click OK. Proof Designer will insert a new gap in the proof,
whose goal is to prove that
, you can type
alt-shift-A (Windows) or option-shift-A (Macintosh) or use the symbol
palette.) Click OK. Proof Designer will insert a new gap in the proof,
whose goal is to prove that 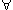 x(x
x(x x).
Note that in the original gap, where you still need to prove that
A
x).
Note that in the original gap, where you still need to prove that
A A, the statement
A, the statement
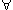 x(x
x(x x) is now listed as a given.
x) is now listed as a given.
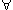 x(x
x(x x) set off from the rest of the proof
as a lemma. (A lemma is a small theorem that is used to prove another
theorem.) To do this, click on the sentence “Proof of
x) set off from the rest of the proof
as a lemma. (A lemma is a small theorem that is used to prove another
theorem.) To do this, click on the sentence “Proof of
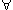 x(x
x(x x) goes here” at the beginning
of the new proof gap. This selects the entire gap. (You can also do this
by clicking in the margin to the left of the gap.) Now choose Lemma from
the Strategy menu.
x) goes here” at the beginning
of the new proof gap. This selects the entire gap. (You can also do this
by clicking in the margin to the left of the gap.) Now choose Lemma from
the Strategy menu.
 x as
x as
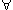 a(a
a(a x
x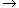 a
a x),
let a be arbitrary, and then do a direct proof of
a
x),
let a be arbitrary, and then do a direct proof of
a x
x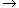 a
a x. Note
that after
you give the Direct command, your goal will already be listed as a given,
so you can select the given and give the Finish command. To fill in the
second gap, you can apply universal instantiation to the given
x. Note
that after
you give the Direct command, your goal will already be listed as a given,
so you can select the given and give the Finish command. To fill in the
second gap, you can apply universal instantiation to the given
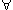 x(x
x(x x) to conclude that
A
x) to conclude that
A A.
A.
 (A)
(A)
 (B)
(B)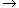 A
A B”,
which selects this conclusion and the subproof that justifies it. Choose
Rejustify from the Edit menu. The subproof and conclusion will disappear,
and be replaced by a gap that says “Proof of
B”,
which selects this conclusion and the subproof that justifies it. Choose
Rejustify from the Edit menu. The subproof and conclusion will disappear,
and be replaced by a gap that says “Proof of
 (A)
(A)
 (B)
(B) A
A B
goes here”. We can now redo the proof a different way. (Leave the
lemma there—we'll need it in this version of the proof too. If you
want, you can hide the details of its proof.)
B
goes here”. We can now redo the proof a different way. (Leave the
lemma there—we'll need it in this version of the proof too. If you
want, you can hide the details of its proof.)
 (A)
(A)
 (B)
(B) A
A B
and choose Contrapositive from the Strategy menu. Proof Designer will
suppose that A
B
and choose Contrapositive from the Strategy menu. Proof Designer will
suppose that A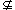 B, and it
will say that you must prove
that
B, and it
will say that you must prove
that  (A)
(A)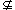
 (B).
(B).
 (A)
(A)
 (B) and choose
Reexpress from the Strategy menu. Click on Apply Definition, but
don't click OK yet. Proof Designer will reexpress the goal as
(B) and choose
Reexpress from the Strategy menu. Click on Apply Definition, but
don't click OK yet. Proof Designer will reexpress the goal as

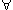 a(a
a(a
 (A)
(A) a
a
 (B)).
Now click Reexpress Negative and Proof Designer will change this to
(B)).
Now click Reexpress Negative and Proof Designer will change this to
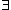 a
a (a
(a
 (A)
(A) a
a
 (B)).
Note that now only
(B)).
Note that now only
 (a
(a
 (A)
(A) a
a
 (B))
is selected, so you can click Reexpress Negative again to change the
statement to
(B))
is selected, so you can click Reexpress Negative again to change the
statement to
 a(a
a(a
 (A)
(A) a
a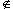
 (B)).
Click OK.
(B)).
Click OK.
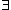 a(a
a(a
 (A)
(A)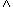 a
a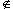
 (B)),
so you should probably try to prove it by finding an example of a set
which is an
element of
(B)),
so you should probably try to prove it by finding an example of a set
which is an
element of  (A) but not
(A) but not  (B), but it may not be clear at
first what set to use. Here's how you can deal with this situation:
Select the goal
(B), but it may not be clear at
first what set to use. Here's how you can deal with this situation:
Select the goal
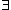 a(a
a(a
 (A)
(A)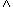 a
a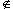
 (B))
and choose Existence from the Strategy menu. A dialog box will appear,
asking what
value you want to substitute for a in the goal. Click on the
“Use this new variable, whose definition will be inserted
later” option. The default choice for the new variable is a,
but if you
want to use a different name you can just type it in. Click OK. You will
now have
two gaps in the proof, one labeled “Definition of a goes
here”,
followed by one labeled “Proof of
a
(B))
and choose Existence from the Strategy menu. A dialog box will appear,
asking what
value you want to substitute for a in the goal. Click on the
“Use this new variable, whose definition will be inserted
later” option. The default choice for the new variable is a,
but if you
want to use a different name you can just type it in. Click OK. You will
now have
two gaps in the proof, one labeled “Definition of a goes
here”,
followed by one labeled “Proof of
a
 (A)
(A)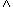 a
a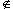
 (B)
goes here”. As usual, you can work on these gaps in either order.
In particular, even before defining a you can start in on the proof
that a
(B)
goes here”. As usual, you can work on these gaps in either order.
In particular, even before defining a you can start in on the proof
that a
 (A)
(A)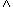 a
a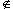
 (B). When you
get far enough in the proof that you can tell what a should be, you
can go
back and fill in the definition of a.
(B). When you
get far enough in the proof that you can tell what a should be, you
can go
back and fill in the definition of a.

 (A)
(A)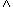 a
a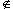
 (B) and give the
Reexpress command from the Strategy menu. Select the statement
a
(B) and give the
Reexpress command from the Strategy menu. Select the statement
a
 (A) and click Apply Definition to change this to
a
(A) and click Apply Definition to change this to
a A. Select a
A. Select a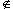
 (B) and click
Apply Definition to change it to
(B) and click
Apply Definition to change it to  a
a B. You
can click
Reexpress Negative if you want to change this to a
B. You
can click
Reexpress Negative if you want to change this to a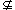 B. Click OK.
B. Click OK.
 A
A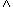 a
a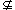 B, and
one of the givens is
A
B, and
one of the givens is
A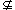 B. This suggests that
perhaps you should have defined
a to be equal to A. Go back to the gap labeled
“Definition of a goes here”, select the goal a = ?,
and choose Define from the
Strategy menu. A dialog box will appear, containing the statement
“Let ___ = ___”. The first blank will already be filled in
with the
default value a. Fill in the second with A and click OK.
The definition
of a will be added to the proof, and the gap labeled
“Definition of
a goes here” will disappear.
B. This suggests that
perhaps you should have defined
a to be equal to A. Go back to the gap labeled
“Definition of a goes here”, select the goal a = ?,
and choose Define from the
Strategy menu. A dialog box will appear, containing the statement
“Let ___ = ___”. The first blank will already be filled in
with the
default value a. Fill in the second with A and click OK.
The definition
of a will be added to the proof, and the gap labeled
“Definition of
a goes here” will disappear.
 A
A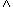 a
a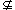 B,
pull down the Strategy menu, and move the mouse down to the Substitute
command, but don't release the mouse button. A submenu will appear,
showing you what substitutions can now be applied. Since we now know
that a = A, you can choose to
substitute either A for a or a for A. Choose
a
B,
pull down the Strategy menu, and move the mouse down to the Substitute
command, but don't release the mouse button. A submenu will appear,
showing you what substitutions can now be applied. Since we now know
that a = A, you can choose to
substitute either A for a or a for A. Choose
a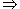 A from the submenu,
indicating that you want to
replace a with A. A dialog box will appear. Click on the
Substitute button and the substitution will be performed. Click OK.
A from the submenu,
indicating that you want to
replace a with A. A dialog box will appear. Click on the
Substitute button and the substitution will be performed. Click OK.
 A
A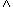 A
A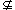 B,
and you already have A
B,
and you already have A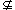 B
in the given column. Select the given
A
B
in the given column. Select the given
A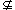 B and the goal
A
B and the goal
A A
A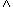 A
A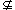 B, and
choose Conjunction from the Infer menu. Proof Designer will use the
conjunction rule of inference to work
backwards from the goal. Proof Designer will say that you can infer
A
B, and
choose Conjunction from the Infer menu. Proof Designer will use the
conjunction rule of inference to work
backwards from the goal. Proof Designer will say that you can infer
A A
A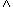 A
A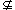 B from
A
B from
A A
and A
A
and A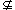 B, but you still
have to prove A
B, but you still
have to prove A A.
A.
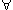 x(x
x(x x) to conclude that A
x) to conclude that A A.
This is your goal, so you can now use the Finish command to complete the
proof.
A.
This is your goal, so you can now use the Finish command to complete the
proof.
Note that we introduced the variable a into this proof only because, at the time we introduced it, we didn't know it would turn out to be equal to A. Now that the proof is done, we could improve on it by eliminating all mention of a, and only talking about A. Often you will be able to improve on the proof outline written by Proof Designer. You should use Proof Designer to work out an outline of a correct proof, and then try to improve on it when you write up the final proof.