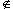 x}
x}
Suppose that “...x...” is some statement about an unspecified object called x. This statement will be true for some values of x and false for others. It is tempting to think that we could form the set of all values of x for which the statement is true. In other words, it is tempting to think that the expression
{x | ...x...}
should be accepted as a definition of a set. However, the assumption that such expressions always name sets leads to a contradiction. This was first noticed by Bertrand Russell in 1901, and so it has come to be known as Russell's Paradox.
To see how the paradox is derived, suppose that all expressions of the type displayed above do name sets. Russell suggested that we consider the following definition of a set R:
R = {x | x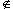 x}
x}
According to this definition, an object x will be an element of
R if and only if x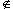 x. But now suppose we ask whether or not R is
an element of itself. Plugging in R for x in the definition
of R, we come to the conclusion that R
x. But now suppose we ask whether or not R is
an element of itself. Plugging in R for x in the definition
of R, we come to the conclusion that R R if and only if R
R if and only if R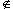 R. But this is impossible; whether R is an
element of itself or not, this statement cannot be true. Thus we have
reached a contradiction.
R. But this is impossible; whether R is an
element of itself or not, this statement cannot be true. Thus we have
reached a contradiction.
The lesson that most mathematicians have drawn from Russell's Paradox is that definitions of the kind displayed above cannot always be trusted to define sets. To avoid the paradox, mathematicians use only a restricted form of this kind of definition. If U is a set, then mathematicians accept the following expression as a definition of a set:
{x U |
...x...}
U |
...x...}
In this definition, only elements of U are considered for membership in the set being defined. Among elements of U, only those that make the statement “...x...” come out true are elements of the set. Following the usual practice in mathematics, Proof Designer only allows definitions of this more restricted kind.
Of course, if U were a set that contained
absolutely everything, then this restricted definition would be equivalent
to the previous, unrestricted one, and would therefore be unacceptable.
Thus, Russell's Paradox can be thought of as a proof that there can be no
set that contains absolutely everything. In fact, this makes a nice,
challenging exercise in Proof Designer! See if you can use Proof Designer
to prove, from no hyptheses, the conclusion 
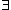 U
U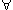 x(x
x(x U).
U).
Russell's Paradox also explains why Proof Designer places a restriction
on intersections of families of sets. If F is a set whose elements
are sets, the  F is the intersection
of all of the sets in F. Thus, for any x, x
F is the intersection
of all of the sets in F. Thus, for any x, x
 F if
and only if
F if
and only if 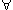 A
A F(x
F(x A).
But if F =
A).
But if F = 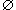 then the statement
then the statement 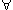 A
A F(x
F(x A)
would be true no matter what x is, and therefore
A)
would be true no matter what x is, and therefore  F would be a set containing everything. Since
Russell's Paradox shows that there can be no such set, it follows that
F would be a set containing everything. Since
Russell's Paradox shows that there can be no such set, it follows that 
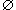 is not a
set. For this reason, Proof Designer requires that you explicitly include
at least one set in any intersection. If U is a set and F is
a family of sets, then U
is not a
set. For this reason, Proof Designer requires that you explicitly include
at least one set in any intersection. If U is a set and F is
a family of sets, then U
 F is the intersection of U and
all of the elements of F. In other words,
F is the intersection of U and
all of the elements of F. In other words,
U
 F = {x
F = {x U |
U | 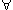 A
A F(x
F(x A)}.
A)}.
Since the values of x in this definition must come from the set U, this definition is acceptable.